Hyperbolic Lattices
Project members: P. M. Lenggenhager, A. Stegmaier, D. M. Urwyler, A. Chen, T. Tummuru, T. Neupert, R. Thomale, J. Maciejko, T. Bzdušek, et. al
Curved spaces are usually associated with high-energy physics and cosmology. However, the possibility of tabletop experiments emulating such phenomena and the interest in synthetic matter in curved spaces have elevated curved spaces to relevance in condensed matter physics as well. Spaces with negative curvature are particularly difficult to realize experimentally. One way to achieve it, is by discretizing the space and implementing the resulting lattice. In this project, we study various aspects of such hyperbolic lattices, both experimentally and theoretically.
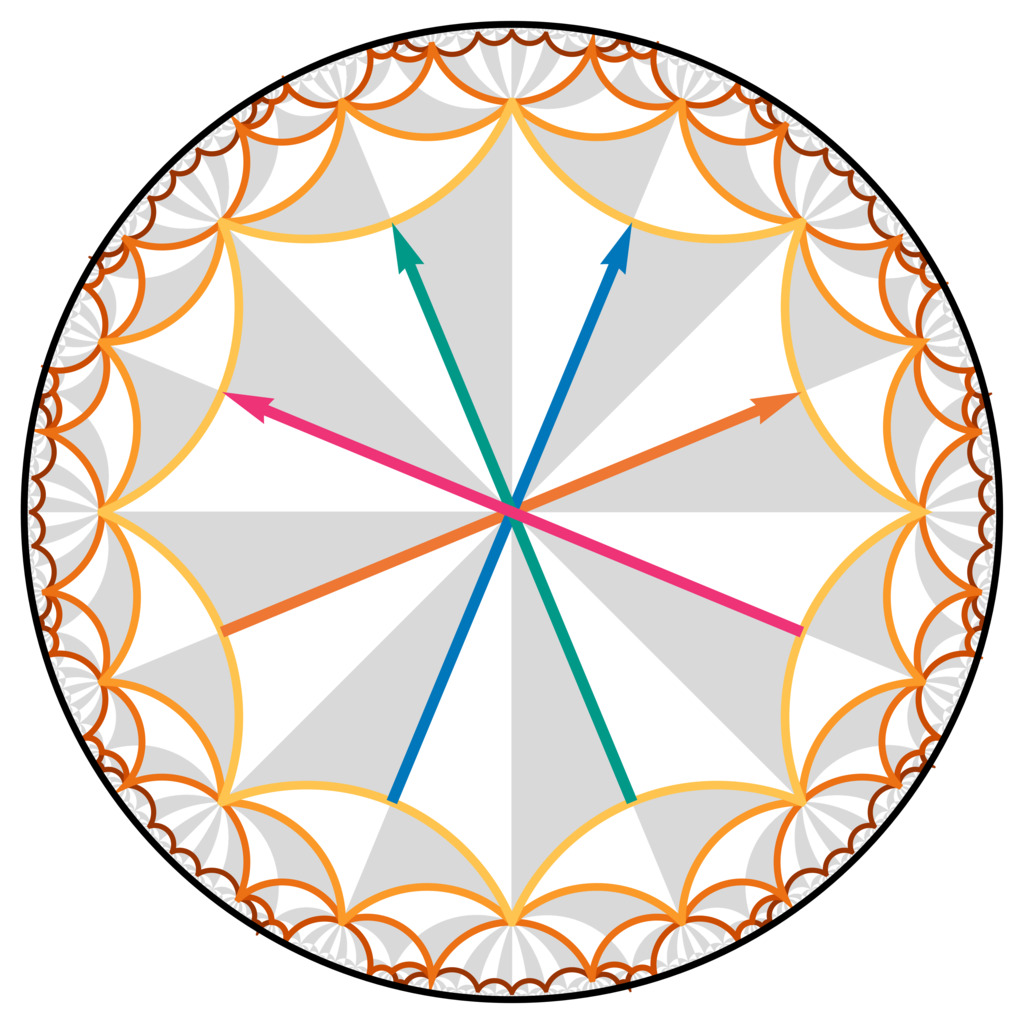
Hyperbolic lattices can be interpreted as tilings of a plane with constant negative curvature. On these lattices one can define tight-binding models of different degrees of complexity. Starting with a simple nearest-neighbor hopping model (with equal and real hopping amplitudes), we demonstrate that such lattices can be realized in electric circuits and that signatures of the negative curvature can be experimentally obtained. Next, we show theoretically that topological models analogous to the Haldane and the Kane-Mele model can be defined on hyperbolic lattices and we study bulk invariants and the bulk-boundary correspondence. Finally, we make progress on developing a band-theoretic description of hyperbolic lattices based on the recent extension of Bloch’s theorem to hyperbolic lattices.
A comprehensive introduction to the topic can be found in my PhD thesis.
Publications
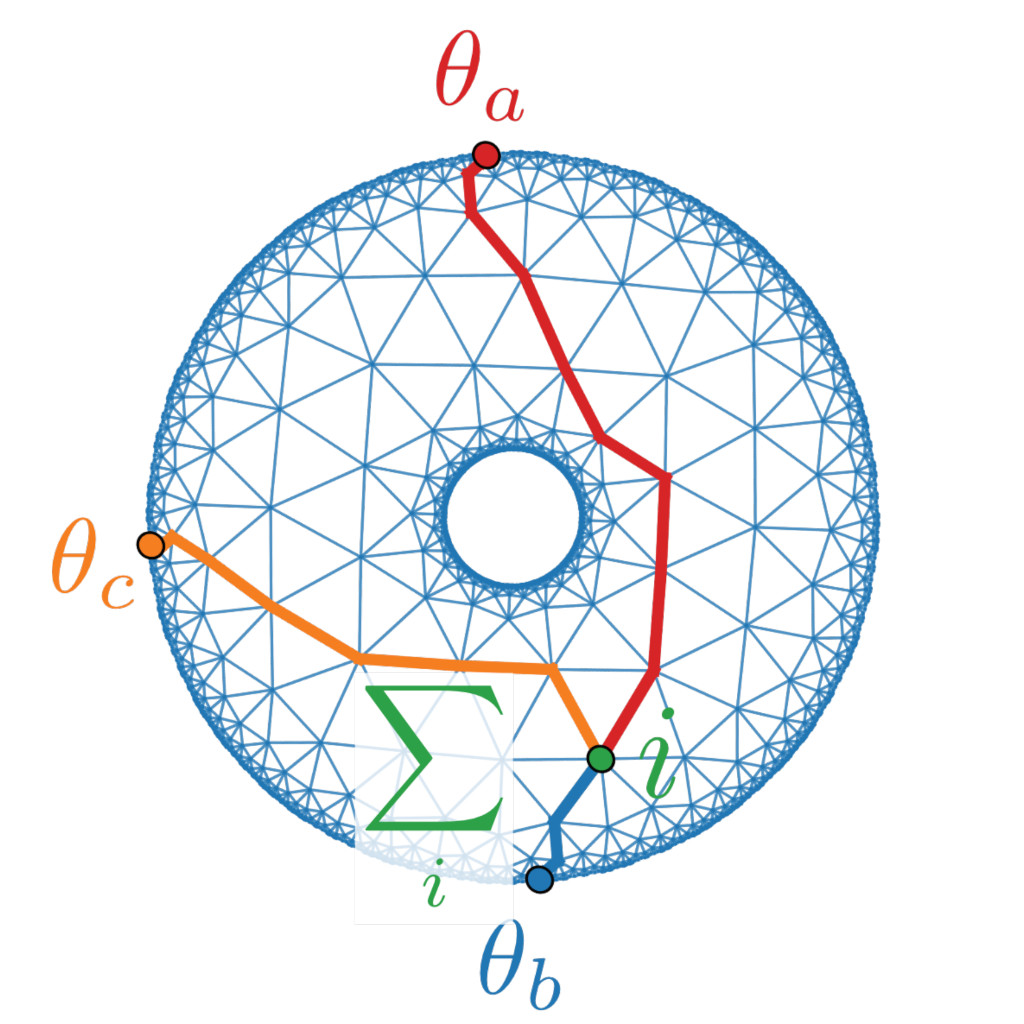
Simulating Holographic Conformal Field Theories on Hyperbolic Lattices
S. Dey, A. Chen, P. Basteiro, A. Fritzsche, M. Greiter, M. Kaminski, P. M. Lenggenhager, R. Meyer, R. Sorbello, A. Stegmaier, R. Thomale, J. Erdmenger, and I. Boettcher, Phys. Rev. Lett. 133, 061603 (2024).
PDF
Hyperbolic Spin Liquids
P. M. Lenggenhager, S. Dey, T. Bzdušek, and J. Maciejko, arXiv:2407.09601 (2024).
PDF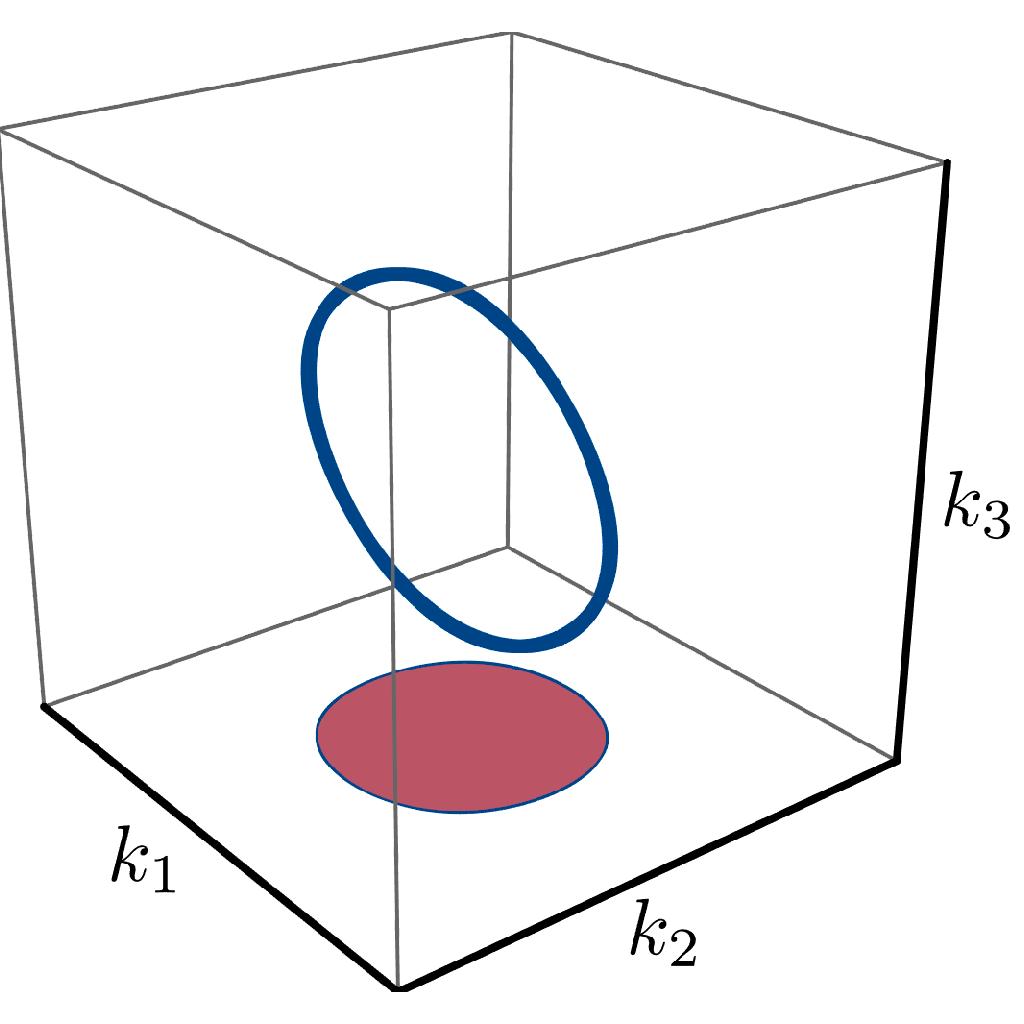
Hyperbolic non-Abelian semimetal
T. Tummuru, A. Chen, P. M. Lenggenhager, T. Neupert, J. Maciejko, and T. Bzdušek, Phys. Rev. Lett. 132, 206601 (2024).
PDF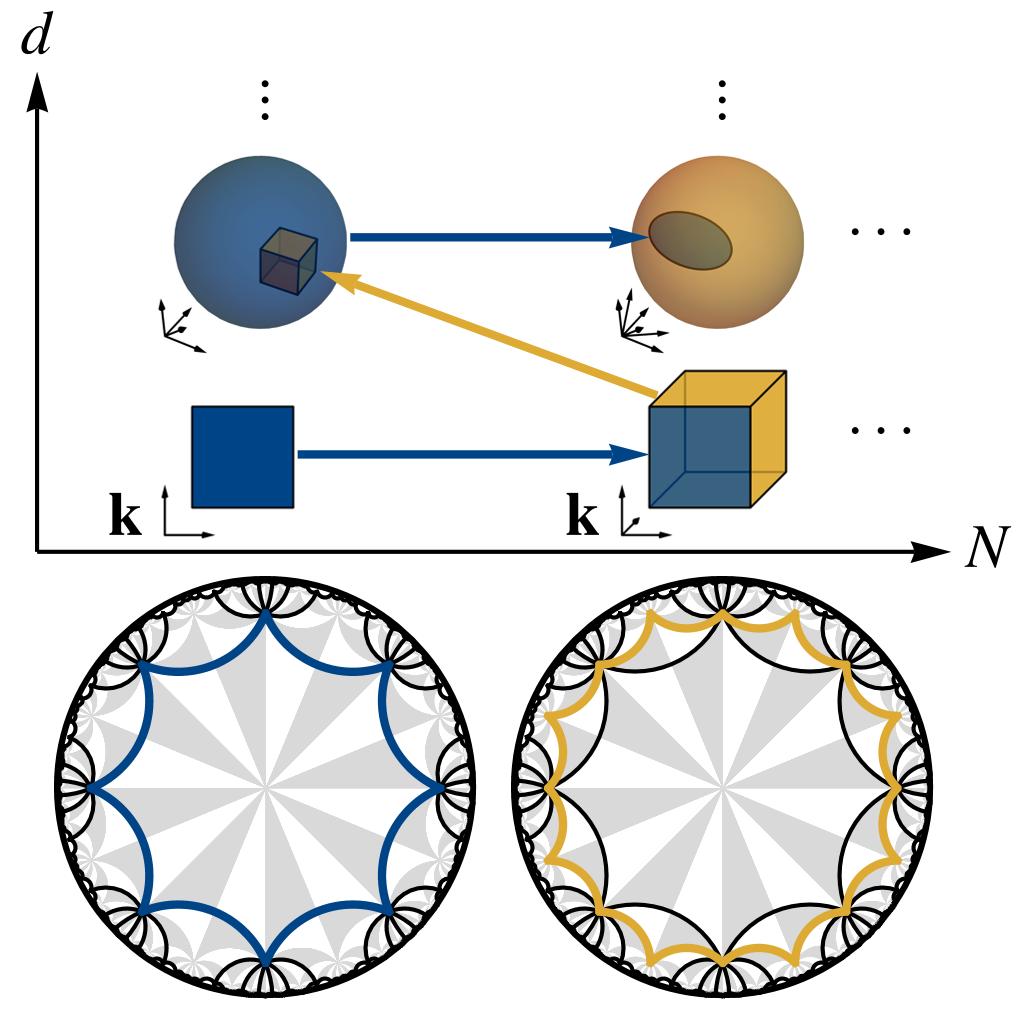
Non-Abelian hyperbolic band theory from supercells
P. M. Lenggenhager, J. Maciejko, and T. Bzdušek, Phys. Rev. Lett. 131, 226401 (2023).
PDF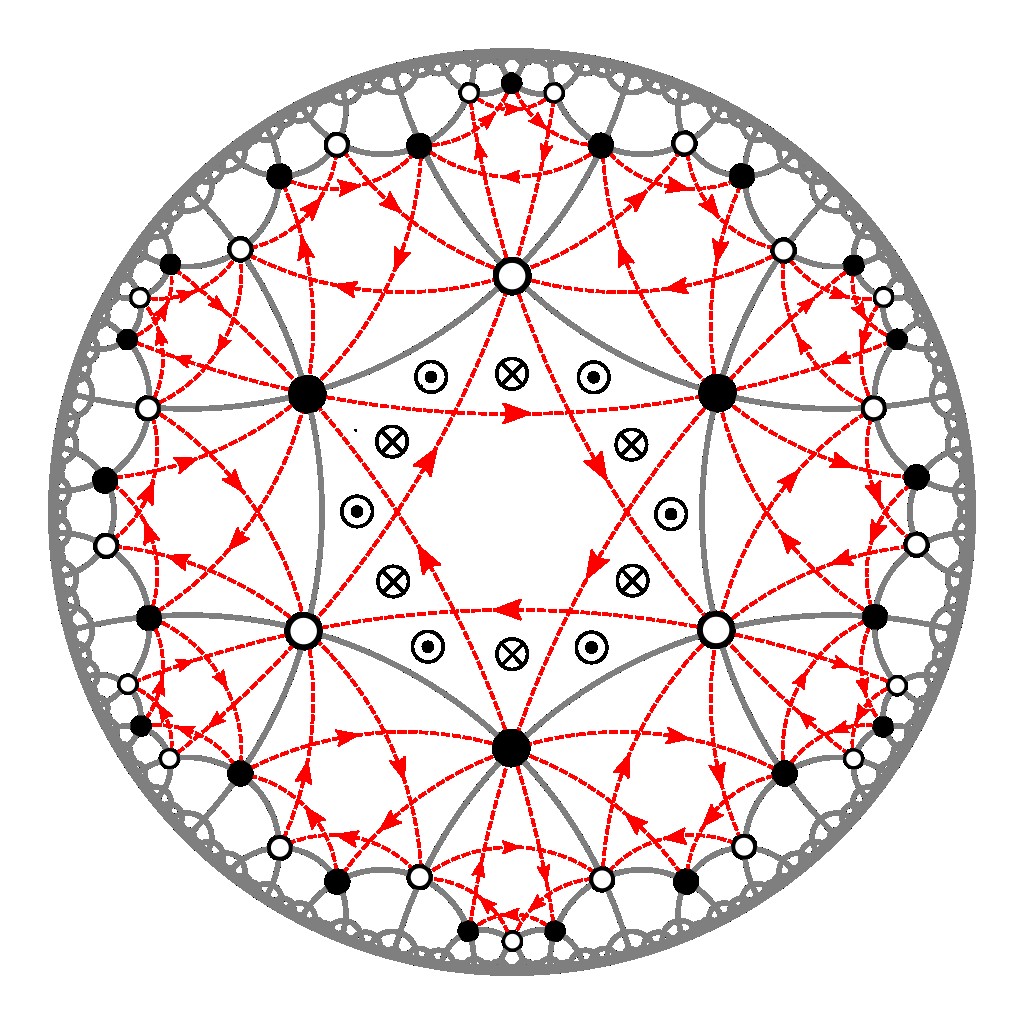
Symmetry and topology of hyperbolic Haldane models
A. Chen, Y. Guan, P. M. Lenggenhager, J. Maciejko, I. Boettcher, and T. Bzdušek, Phys. Rev. B 108, 085114 (2023).
PDF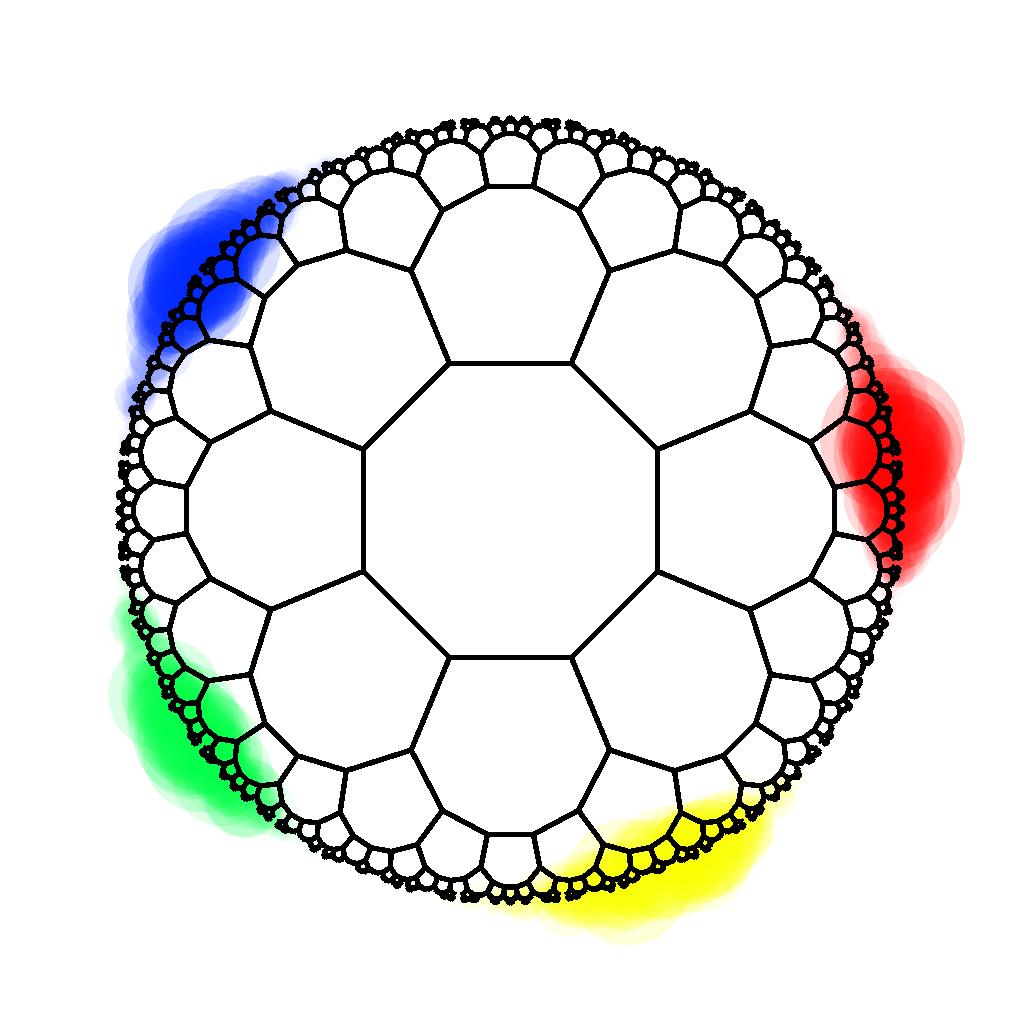
Hyperbolic topological band insulators
D. M. Urwyler, P. M. Lenggenhager, I. Boettcher, R. Thomale, T. Neupert, and T. Bzdušek, Phys. Rev. Lett. 129, 246402 (2022).
PDF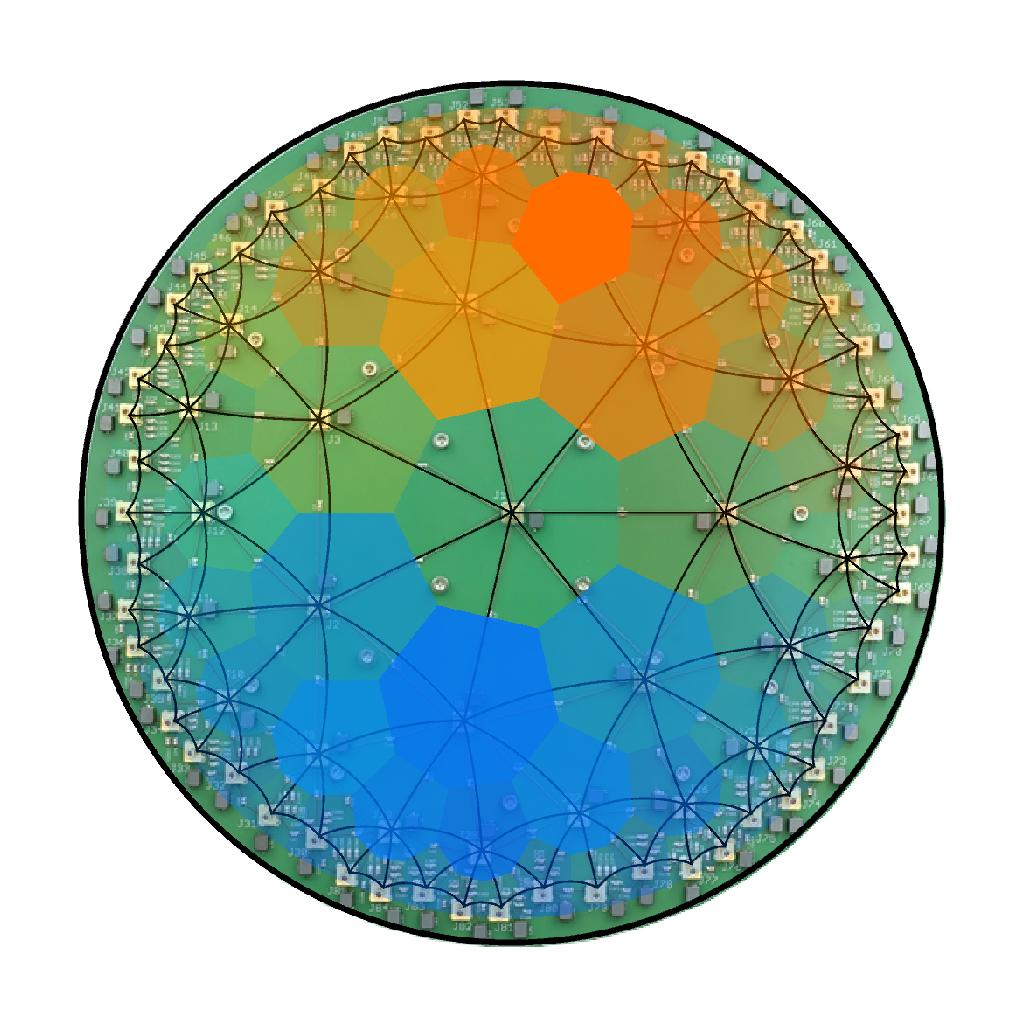
Simulating hyperbolic space on a circuit board
P. M. Lenggenhager, A. Stegmaier, L. K. Upreti, T. Hofmann, T. Helbig, A. Vollhardt, M. Greiter, C. H. Lee, S. Imhof, H. Brand, T. Kießling, I. Boettcher, T. Neupert, R. Thomale, and T. Bzdušek, Nat. Commun. 13, 4373 (2022).
PDF