@article{Chen:2023,
  title               = {Symmetry and topology of hyperbolic {H}aldane models}, 
  author              = {Chen, Anffany and Guan, Yifei and Lenggenhager, Patrick M. and Maciejko, Joseph and Boettcher, Igor and Bzdu\v{s}ek, Tom\'{a}\v{s}},
  journal             = {Phys. Rev. B},
  volume              = {108},
  issue               = {8},
  pages               = {085114},
  numpages            = {42},
  year                = {2023},
  month               = {8},
  publisher           = {American Physical Society},
  doi                 = {10.1103/PhysRevB.108.085114}
}

A. Chen, Y. Guan, P. M. Lenggenhager, J. Maciejko, I. Boettcher, and T. Bzdušek

Phys. Rev. B 108, 085114 (2023) – Published 11 Aug 2023

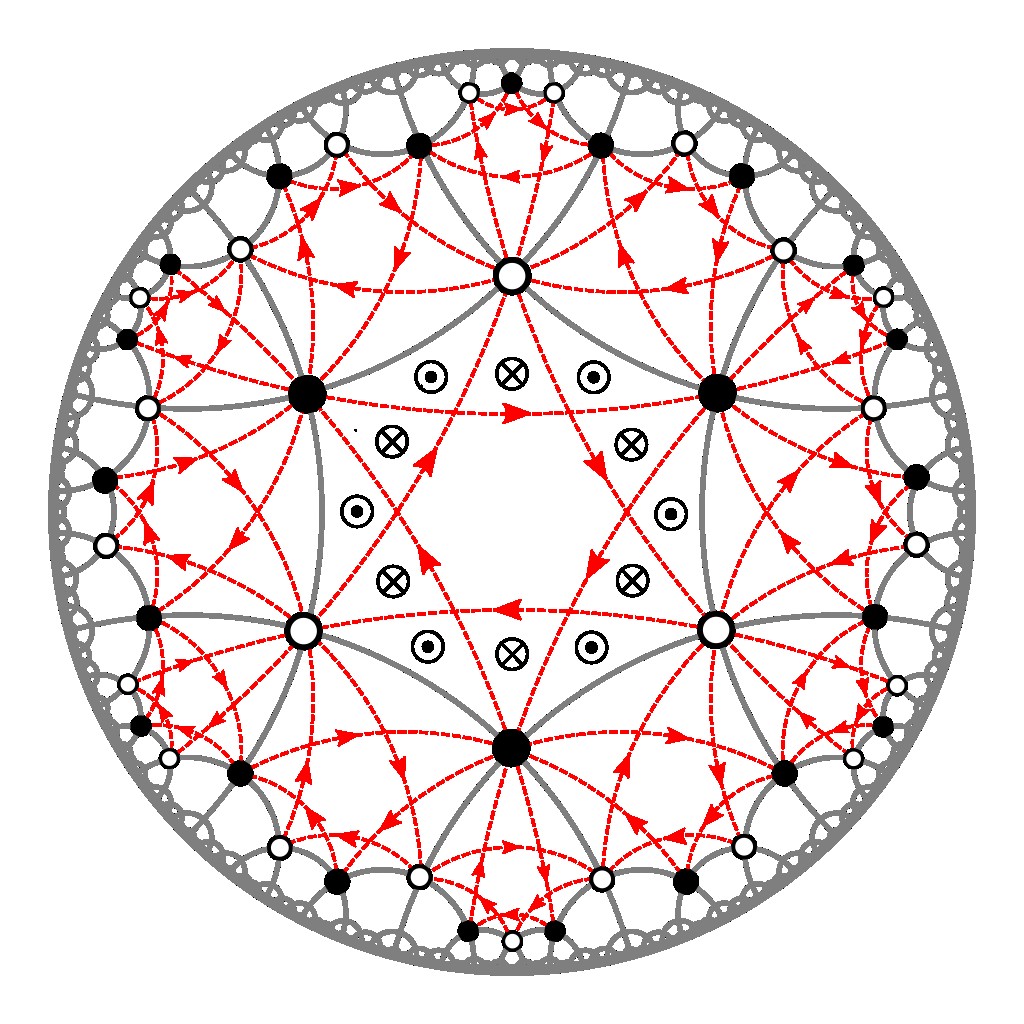
Particles hopping on a two-dimensional hyperbolic lattice feature unconventional energy spectra and wave functions that provide a largely uncharted platform for topological phases of matter beyond the Euclidean paradigm. Using real-space topological markers as well as Chern numbers defined in the higher-dimensional momentum space of hyperbolic band theory, we construct and investigate hyperbolic Haldane models, which are generalizations of Haldane’s honeycomb-lattice model to various hyperbolic lattices. We present a general framework to characterize point-group symmetries in hyperbolic tight-binding models, and use this framework to constrain the multiple first and second Chern numbers in momentum space. We observe several topological gaps characterized by first Chern numbers of value 1 and 2. The momentum-space Chern numbers respect the predicted symmetry constraints and agree with real-space topological markers, indicating a direct connection to observables such as the number of chiral edge modes. With our large repertoire of models, we further demonstrate that the topology of hyperbolic Haldane models is trivialized for lattices with strong negative curvature.