@article{Tummuru:2024,
  title               = {Hyperbolic non-Abelian semimetal}, 
  author              = {Tarun Tummuru and Anffany Chen and Patrick M. Lenggenhager and Titus Neupert and Joseph Maciejko and Tom\'{a}\v{s} Bzdu\v{s}ek},
  journal             = {arXiv preprint},
  journal             = {Phys. Rev. Lett.},
  volume              = {132},
  issue               = {20},
  pages               = {206601},
  numpages            = {7},
  year                = {2024},
  month               = {May},
  publisher           = {American Physical Society},
  doi                 = {10.1103/PhysRevLett.132.206601},
}

T. Tummuru, A. Chen, P. M. Lenggenhager, T. Neupert, J. Maciejko, and T. Bzdušek

Phys. Rev. Lett. 132, 206601 (2024) – Published 14 May 2024

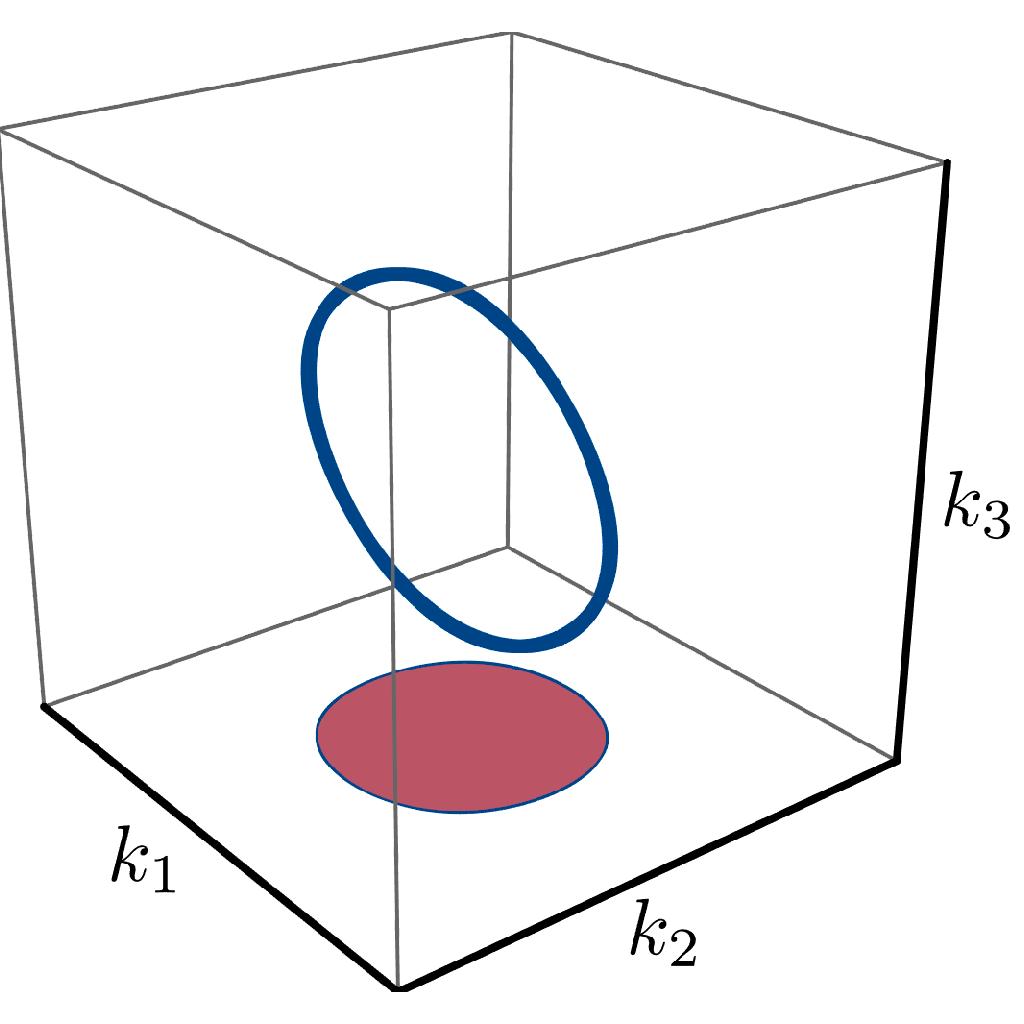
We extend the notion of topologically protected semi-metallic band crossings to hyperbolic lattices in a negatively curved plane. Because of their distinct translation group structure, such lattices are associated with a high-dimensional reciprocal space. In addition, they support non-Abelian Bloch states which, unlike conventional Bloch states, acquire a matrix-valued Bloch factor under lattice translations. Combining diverse numerical and analytical approaches, we uncover an unconventional scaling in the density of states at low energies, and illuminate a nodal manifold of codimension five in the reciprocal space. The nodal manifold is topologically protected by a nonzero second Chern number, reminiscent of the characterization of Weyl nodes by the first Chern number.

Check out this Wolfram community post which has been selected for the editorial columns Staff Picks and Publication Materials. In that post, I demonstrate how to use Mathematica and our software packages HyperCells and HyperBloch to define the model we study and analyze it using the supercell method.