@article{Lenggenhager:2022a,
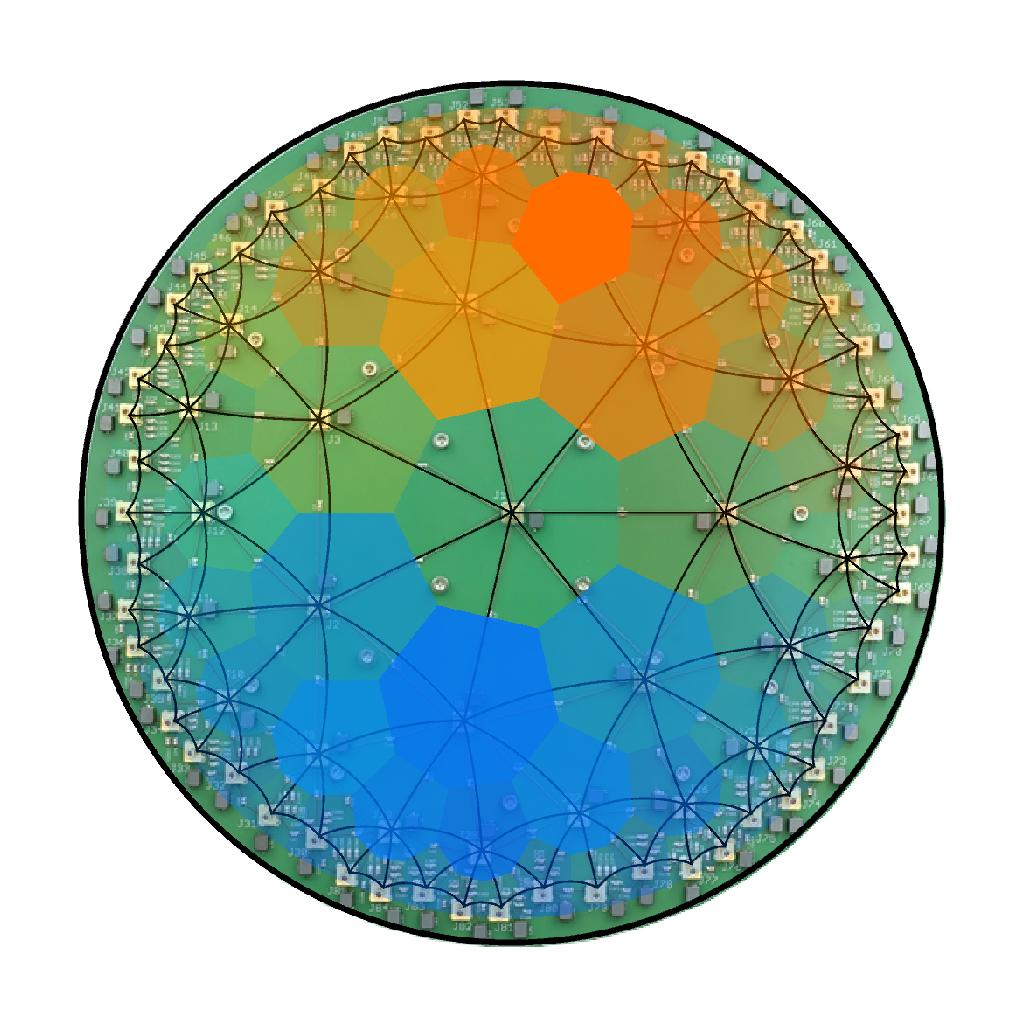
  title               = {Simulating hyperbolic space on a circuit board}, 
  author              = {Lenggenhager, Patrick M. and Stegmaier, Alexander and Upreti, Lavi K. and Hofmann, Tobias and Helbig, Tobias and Vollhardt, Achim and Greiter, Martin and Lee, Ching Hua and Imhof, Stefan and Brand, Hauke and Kie{\ss}ling, Tobias and Boettcher, Igor and Neupert, Titus and Thomale, Ronny and Bzdu\v{s}ek, Tom\'{a}\v{s}},
  journal             = {Nature Communications},
  volume              = {13},
  pages               = {4373},
  issn                = {2041-1723},
  number              = {1},
  year                = {2022},
  doi                 = {10.1038/s41467-022-32042-4},
  url                 = {https://doi.org/10.1038/s41467-022-32042-4},
}

P. M. Lenggenhager, A. Stegmaier, L. K. Upreti, T. Hofmann, T. Helbig, A. Vollhardt, M. Greiter, C. H. Lee, S. Imhof, H. Brand, T. Kießling, I. Boettcher, T. Neupert, R. Thomale, and T. Bzdušek

Nat. Commun. 13, 4373 (2022) – Published 28 Jul 2022

Spaces with negative curvature are particularly difficult to realize experimentally. We show how to emulate a discretized version of constant negatively curved space, a so called hyperbolic lattice, using an electric circuit network. We present static and dynamical methods which allowed us to characterize and verify the negative curvature in the implemented model. Our experiments showcase a versatile platform to emulate hyperbolic lattices in tabletop experiments, which can be utilized to explore propagation dynamics as well as to realize topological hyperbolic matter.

Abstract

The Laplace operator encodes the behaviour of physical systems at vastly different scales, describing heat flow, fluids, as well as electric, gravitational, and quantum fields. A key input for the Laplace equation is the curvature of space. Here we demonstrate that the spectral ordering of Laplacian eigenstates for hyperbolic (negative curvature) and flat (zero curvature) two-dimensional spaces has a universally different structure. We use a lattice representation of hyperbolic space in an electric-circuit network to measure the eigenstates of a ‘hyperbolic drum’, and to analyze signal propagation along the curved geodesics. Our experiments showcase a versatile platform to emulate hyperbolic lattices in tabletop experiments, which can be utilized to explore propagation dynamics as well as to realize topological hyperbolic matter.

Check out this Staff Picks Wolfram community post demonstrating how we obtained the theoretical results and analyzed the experimental data using Mathematica.