Projects
P. M. Lenggenhager, S. Dey, T. Tummuru, A. Chen, D. M. Urwyler, A. Stegmaier, T. Neupert, R. Thomale, J. Maciejko, T. Bzdušek, et. al
P. M. Lenggenhager, S. Dey, T. Tummuru, A. Chen, D. M. Urwyler, A. Stegmaier, T. Neupert, R. Thomale, J. Maciejko, T. Bzdušek, et. al
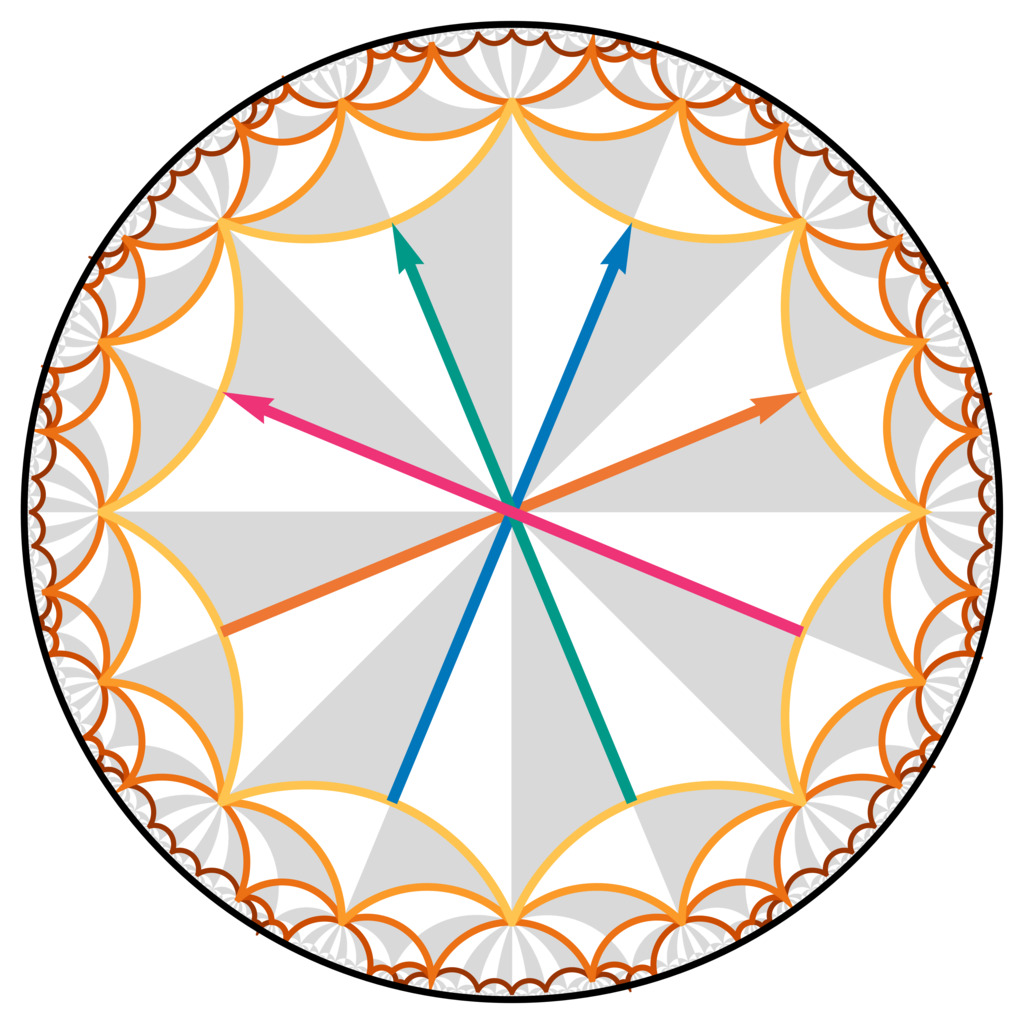
Curved spaces are usually associated with high-energy physics and cosmology. However, the possibility of tabletop experiments emulating such phenomena and the interest in synthetic matter in curved spaces have elevated curved spaces to relevance in condensed matter physics as well. Spaces with negative curvature are particularly difficult to realize experimentally. One way to achieve it, is by discretizing the space and implementing the resulting lattice. In this project, we study various aspects of such hyperbolic lattices, both experimentally and theoretically.
P. M. Lenggenhager, S. Dey, T. Tummuru, A. Chen, D. M. Urwyler, A. Stegmaier, T. Neupert, R. Thomale, J. Maciejko, T. Bzdušek, et. al
P. M. Lenggenhager, S. Dey, T. Tummuru, A. Chen, D. M. Urwyler, A. Stegmaier, T. Neupert, R. Thomale, J. Maciejko, T. Bzdušek, et. al


Curved spaces are usually associated with high-energy physics and cosmology. However, the possibility of tabletop experiments emulating such phenomena and the interest in synthetic matter in curved spaces have elevated curved spaces to relevance in condensed matter physics as well. Spaces with negative curvature are particularly difficult to realize experimentally. One way to achieve it, is by discretizing the space and implementing the resulting lattice. In this project, we study various aspects of such hyperbolic lattices, both experimentally and theoretically.

P. M. Lenggenhager, X. Liu, S. S. Tsirkin, T. Neupert, and T. Bzdušek
P. M. Lenggenhager, X. Liu, S. S. Tsirkin, T. Neupert, and T. Bzdušek
In this project, we study triple nodal points, i.e., three-fold degeneracies of energy bands in the momentum space of three-dimensional crystalline solids. Based on symmetries required for their stability, we haved developed a classification of triple nodal points in spinless systems. By combining the derived classification with symmetry indicators for corner charges, we have further proven that pairs of triple points in semimetals are associated with monopole charges and higher-order topology. We also discuss the various phase transitions occurring when symmetries are broken and present results obtained from first-principles on real materials supporting our findings.
P. M. Lenggenhager, X. Liu, S. S. Tsirkin, T. Neupert, and T. Bzdušek
P. M. Lenggenhager, X. Liu, S. S. Tsirkin, T. Neupert, and T. Bzdušek


In this project, we study triple nodal points, i.e., three-fold degeneracies of energy bands in the momentum space of three-dimensional crystalline solids. Based on symmetries required for their stability, we haved developed a classification of triple nodal points in spinless systems. By combining the derived classification with symmetry indicators for corner charges, we have further proven that pairs of triple points in semimetals are associated with monopole charges and higher-order topology. We also discuss the various phase transitions occurring when symmetries are broken and present results obtained from first-principles on real materials supporting our findings.