@article{Lenggenhager:2025,
    title               = {Hyperbolic Spin Liquids}, 
    author              = {Patrick M. Lenggenhager, Santanu Dey, Tomáš Bzdušek, Joseph Maciejko},
    journal             = {Phys. Rev. Lett.},
    volume              = {135},
    issue               = {7},
    pages               = {076604},
    numpages            = {10},
    year                = {2025},
    month               = {Aug},
    publisher           = {American Physical Society},
    doi                 = {10.1103/s25y-s4fj},
    url                 = {https://link.aps.org/doi/10.1103/s25y-s4fj}
}

P. M. Lenggenhager, S. Dey, T. Bzdušek, and J. Maciejko

Phys. Rev. Lett. 135, 076604 (2025) – Published 15 Aug 2025

Hyperbolic lattices present a unique opportunity to venture beyond the conventional paradigm of crystalline many-body physics and explore correlated phenomena in negatively curved space. As a theoretical benchmark for such investigations, we extend Kitaev’s spin-1/2 honeycomb model to hyperbolic lattices and exploit their non-Euclidean space-group symmetries to solve the model exactly. We elucidate the ground-state phase diagram on the \(\{8,3\}\) lattice and find a gapped \(\mathbb{Z}_2\) spin liquid with Abelian anyons, a gapped chiral spin liquid with non-Abelian anyons and chiral edge states, and a Majorana metal whose finite low-energy density of states is dominated by non-Abelian Bloch states.

The following animation shows the evolution of the phase diagram of the hyperbolic Kitaev model on the \(\{8,3\}\) lattice with magnetic field (three-spin interaction; green dashed lines on the left) \(K\):

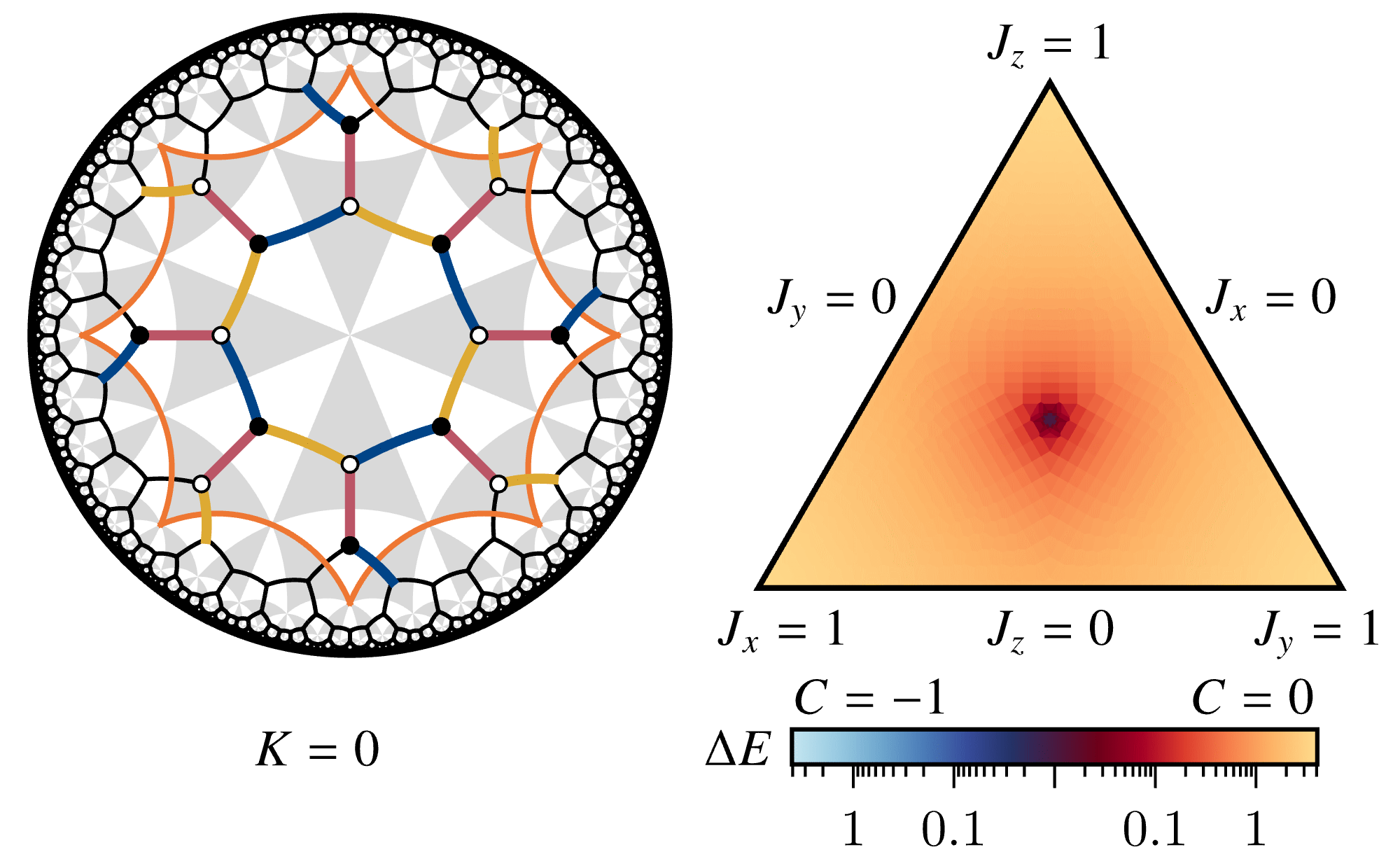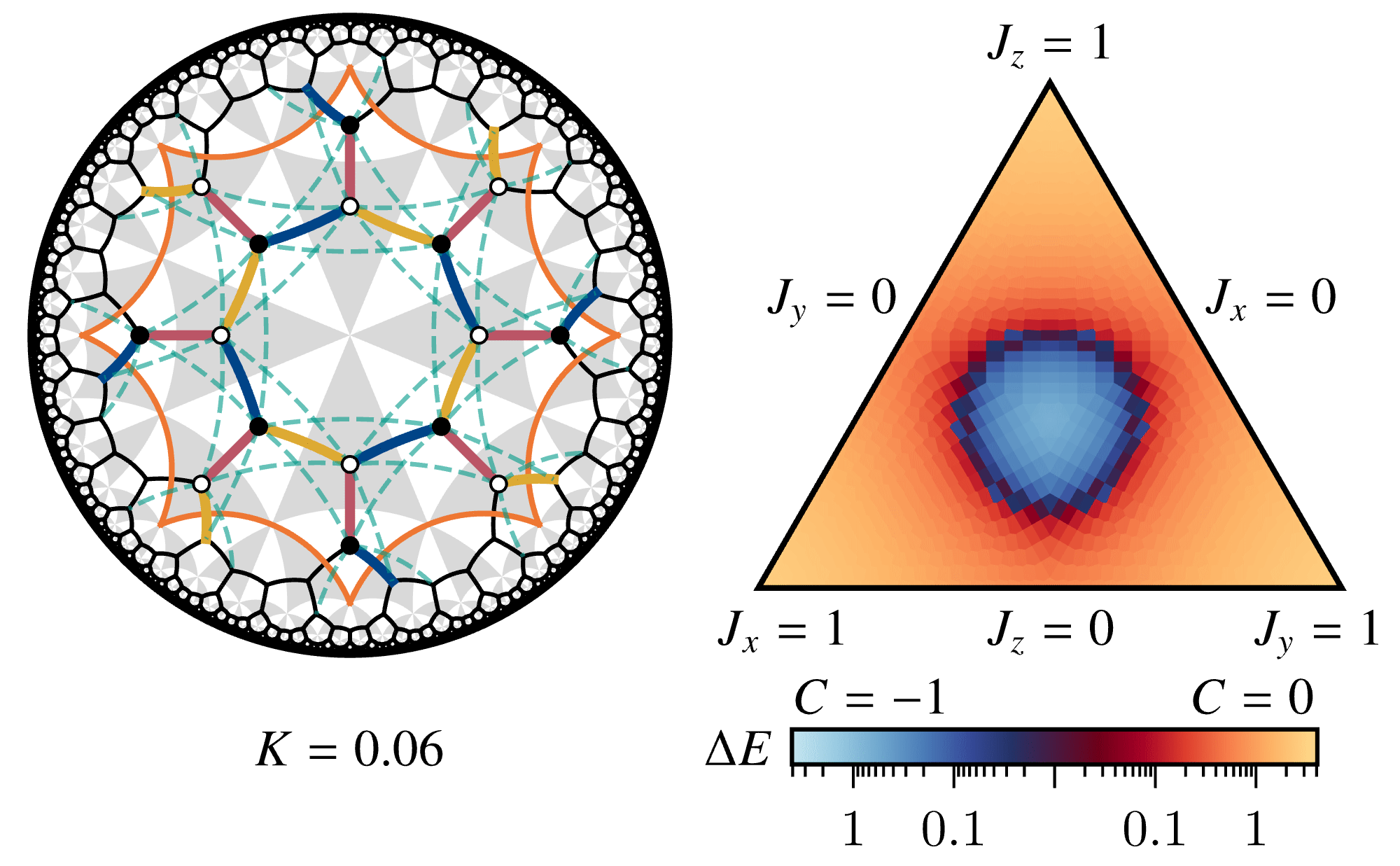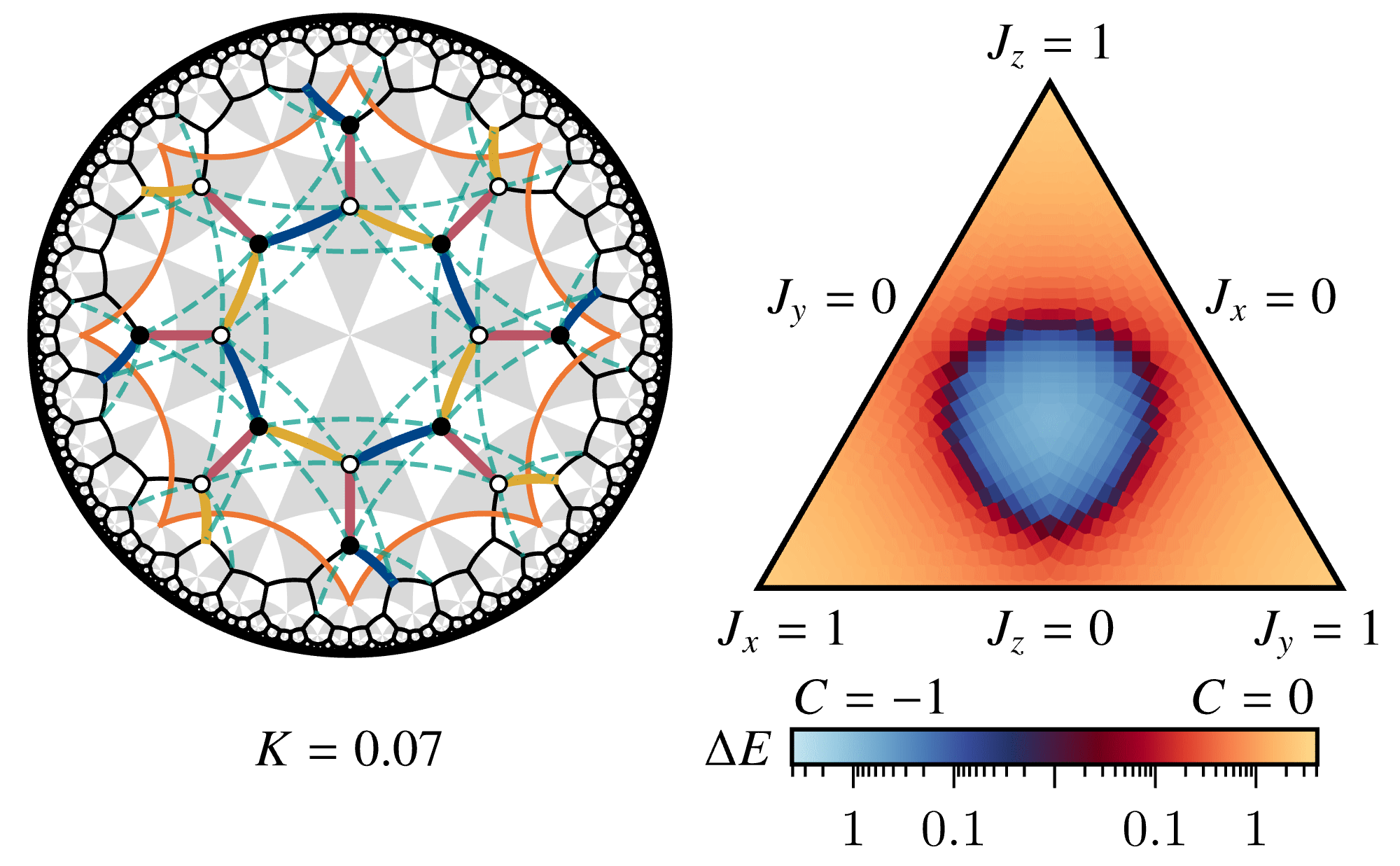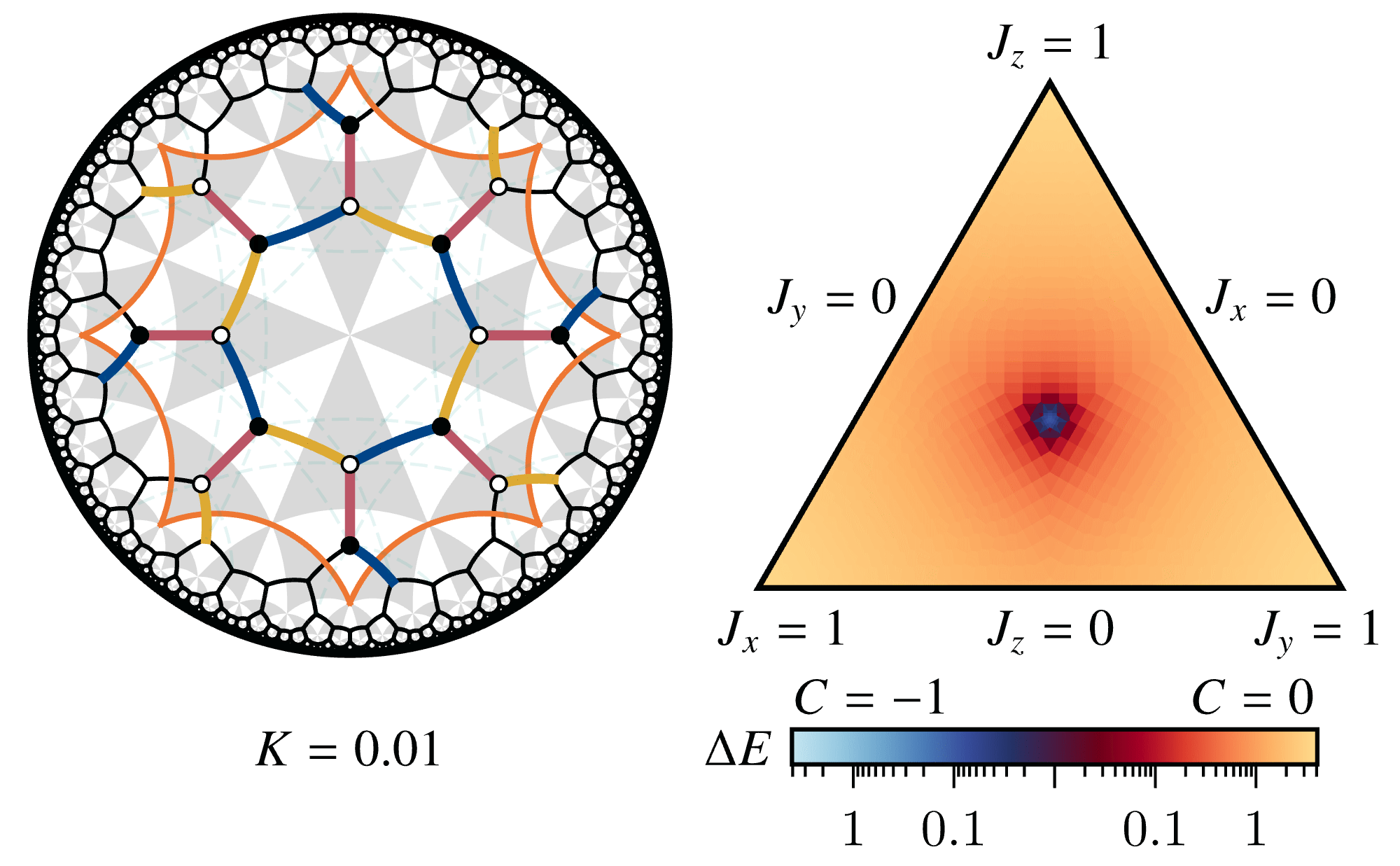
The left panel illustrates the definition of the model in the primary unit cell (orange octagon), in particular the symmetric three-edge coloring. The phase diagram on the right shows both the fermionic spectral gap \(\Delta E\) and the Chern number \(C\) (legend on the bottom) as a function of the interaction strengths \(J_x\), \(J_y\), \(J_z\) on the colored bonds. For \(K>0\), a gapped chiral spin liquid (Chern number \(C=-1\); blue region) with non-Abelian anyons and chiral edge states emerges and grows with increasing magnitude \(K\).

Check out this Wolfram community post which has been selected for the editorial columns Staff Picks and Publication Materials. In that post, I demonstrate how to use Mathematica and our software packages HyperCells and HyperBloch to define the hyperbolic Kitaev model and analyze it using the supercell method.