Classification and Topology of Triple Nodal Points
Project members: P. M. Lenggenhager, X. Liu, S. S. Tsirkin, T. Neupert, and T. Bzdušek




In this project, we study triple nodal points, i.e., three-fold degeneracies of energy bands in the momentum space of three-dimensional crystalline solids. Based on symmetries required for their stability, we haved developed a classification of triple nodal points in spinless systems. By combining the derived classification with symmetry indicators for corner charges, we have further proven that pairs of triple points in semimetals are associated with monopole charges and higher-order topology. We also discuss the various phase transitions occurring when symmetries are broken and present results obtained from first-principles on real materials supporting our findings.
Introduction
Triple nodal points are degeneracies of energy bands in momentum space at which three Hamiltonian eigenstates coalesce at a single eigenenergy. For spinless particles, the stability of a triple nodal point requires two ingredients: (1) rotation symmetry of order three, four or six (or rotation symmetry of order four or six combined with space-time inversion symmery) and (2) mirror or space-time-inversion symmetry.
Summary of Results
We have classified triple points in all (magnetic) space groups, including the non-symmorphic ones, based on the little co-group of the high-symmetry line along which they occur and the irreducible co-representations of the bands that are involved as type \(\mathsf{A}\) vs. type \(\mathsf{B}_l\) vs. type \(\mathsf{B}_q\) depending on whether there are no additional nodal lines attached to the triple point vs. nodal lines attaching linearly vs. nodal lines attaching quadratically to the triple point. Futhermore, we have analyzed the nodal-line structure near triple points, in particular nodal-line arcs coalescing at the high-symmetry line forming nexus points. For type-\(\mathsf{A}\) triple points in systems with space-time inversion symmetry, we found that the nodal line along the high-symmetry line on which they occur carries a non-Abelian topological invariant which explains the conversion of the triple-point into a multiband nodal link when the rotation symmetry is broken. Finally, we have studied triple-point pairs (two triple points that are formed by two consecutive bands crossing the central nodal line) and showed that they induce higher-order topology, i.e. topology with signatures not on the surface but on the hinges.
For more information, please have a look at the papers listed below.
Publications
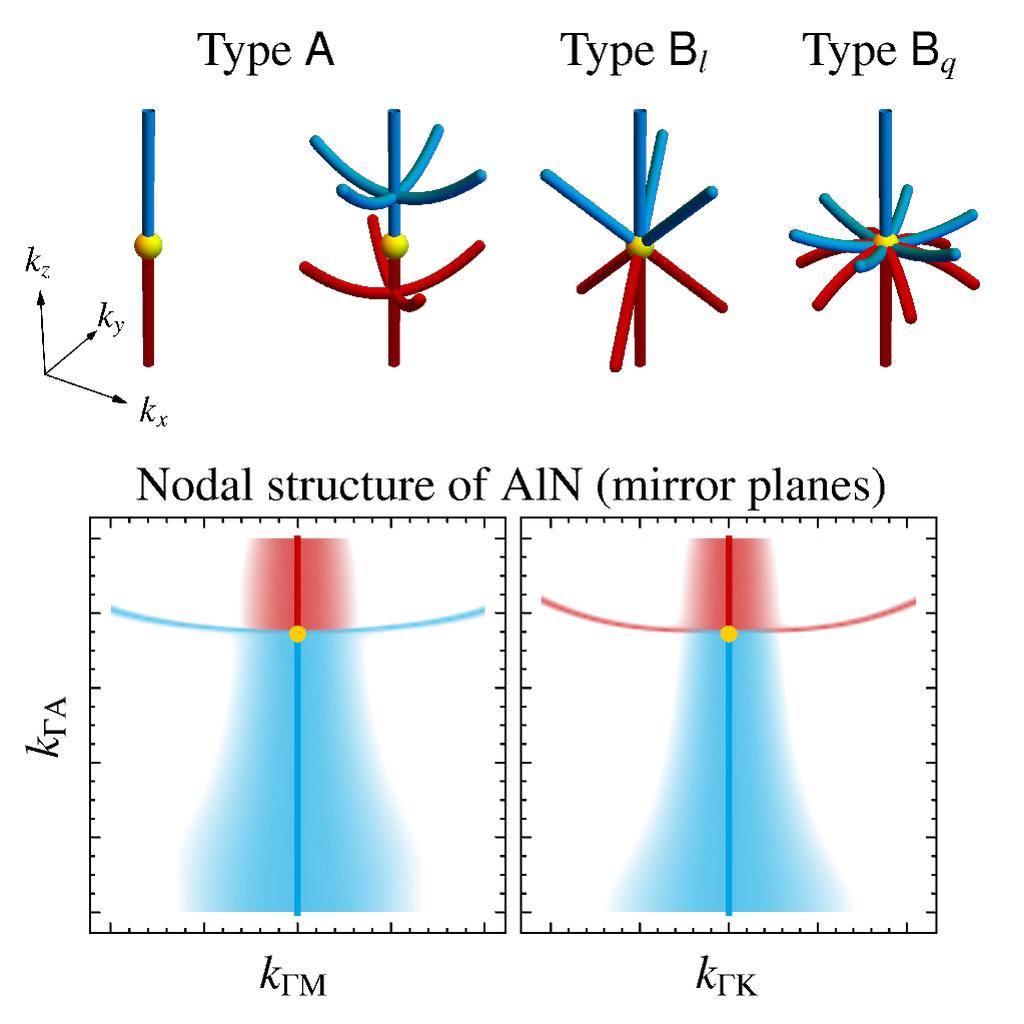
Triple nodal points characterized by their nodal-line structure in all magnetic space groups
P. M. Lenggenhager, X. Liu, T. Neupert, and T. Bzdušek, Phys. Rev. B 106, 085128 (2022).
PDF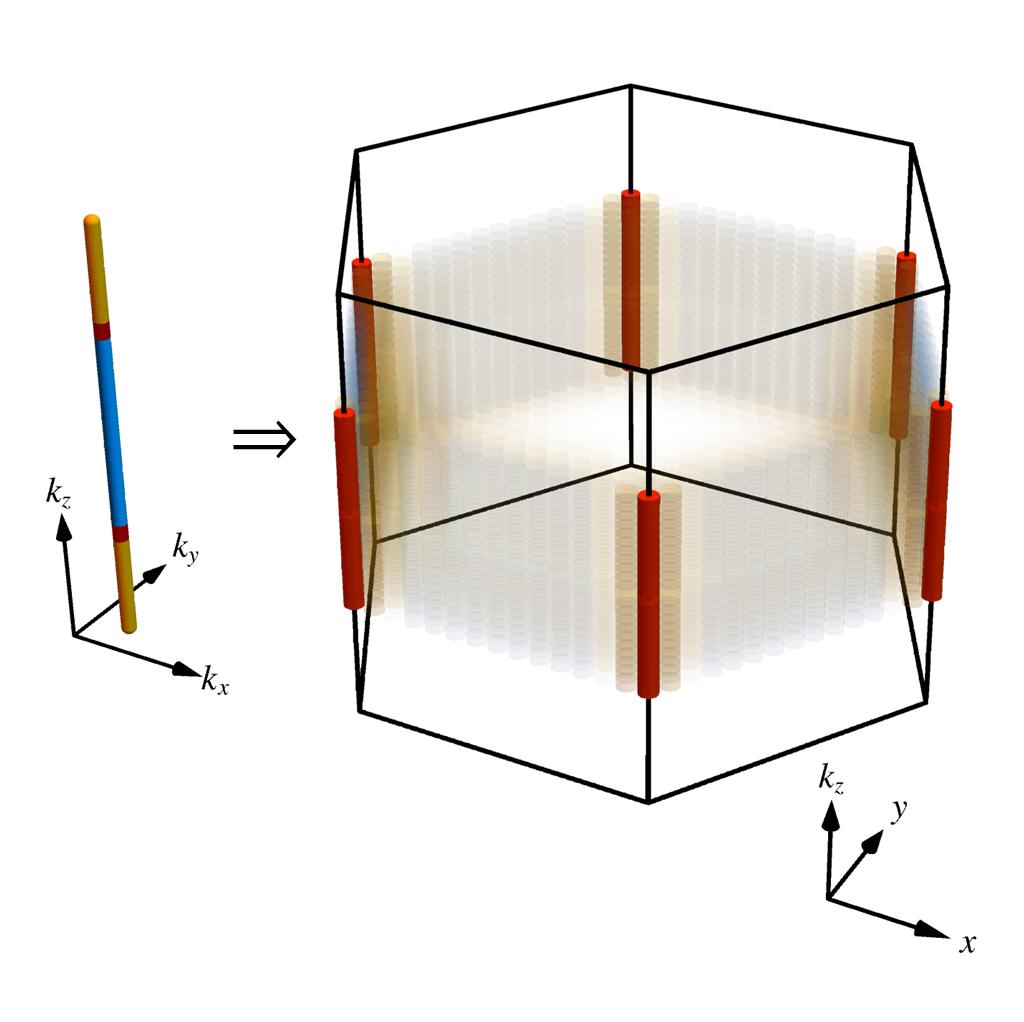
Universal higher-order bulk-boundary correspondence of triple nodal points
P. M. Lenggenhager, X. Liu, T. Neupert, and T. Bzdušek, Phys. Rev. B 106, 085129 (2022).
PDF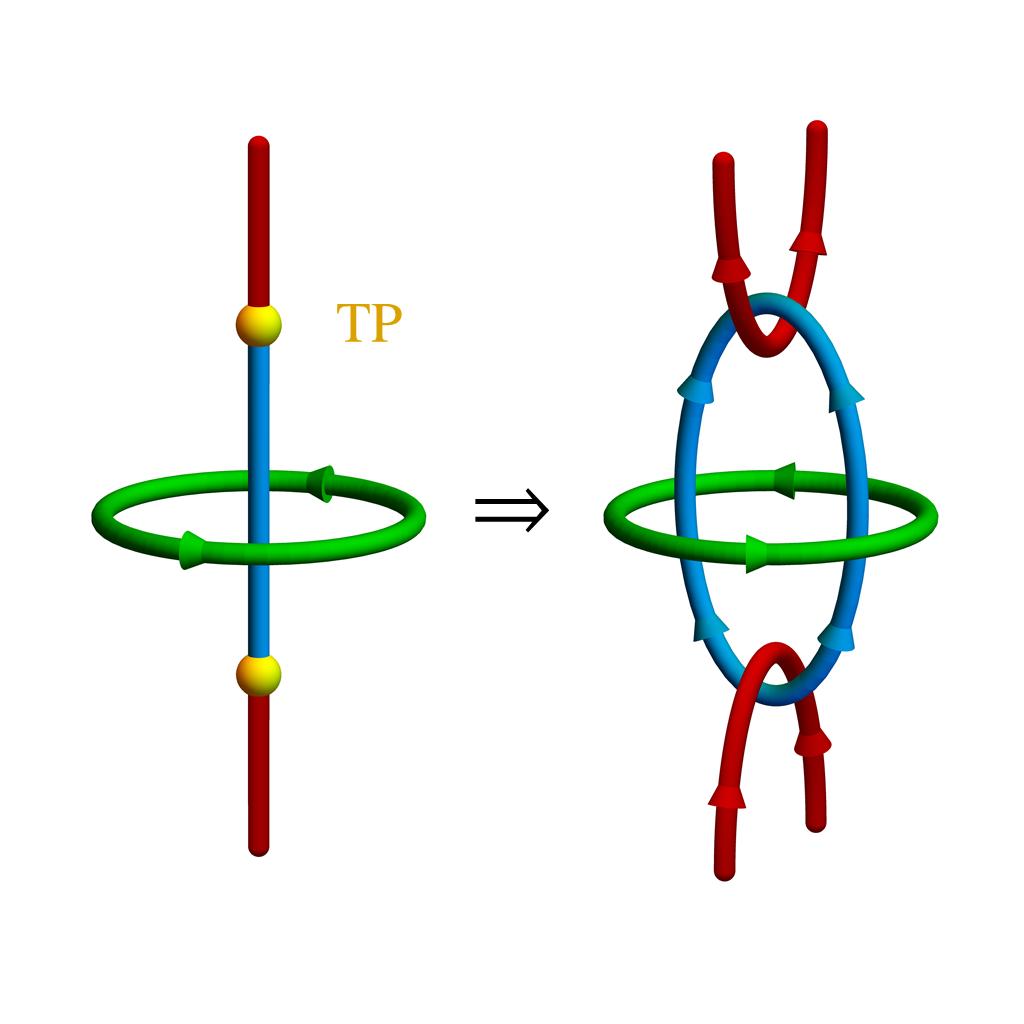
From triple-point materials to multiband nodal links
P. M. Lenggenhager, X. Liu, S. S. Tsirkin, T. Neupert, and T. Bzdušek, Phys. Rev. B 103, L121101 (2021).
PDF