@article{Lenggenhager:2022c,
  title               = {Universal higher-order bulk-boundary correspondence of triple nodal points}, 
  author              = {Lenggenhager, Patrick M. and Liu, Xiaoxiong and Neupert, Titus and Bzdu\v{s}ek, Tom\'{a}\v{s}},
  journal             = {Phys. Rev. B},
  volume              = {106},
  issue               = {8},
  pages               = {085129},
  numpages            = {43},
  year                = {2022},
  month               = {Aug},
  publisher           = {American Physical Society},
  doi                 = {10.1103/PhysRevB.106.085129},
  url                 = {https://link.aps.org/doi/10.1103/PhysRevB.106.085129}
}

P. M. Lenggenhager, X. Liu, T. Neupert, and T. Bzdušek

Phys. Rev. B 106, 085129 (2022) – Published 18 Aug 2022

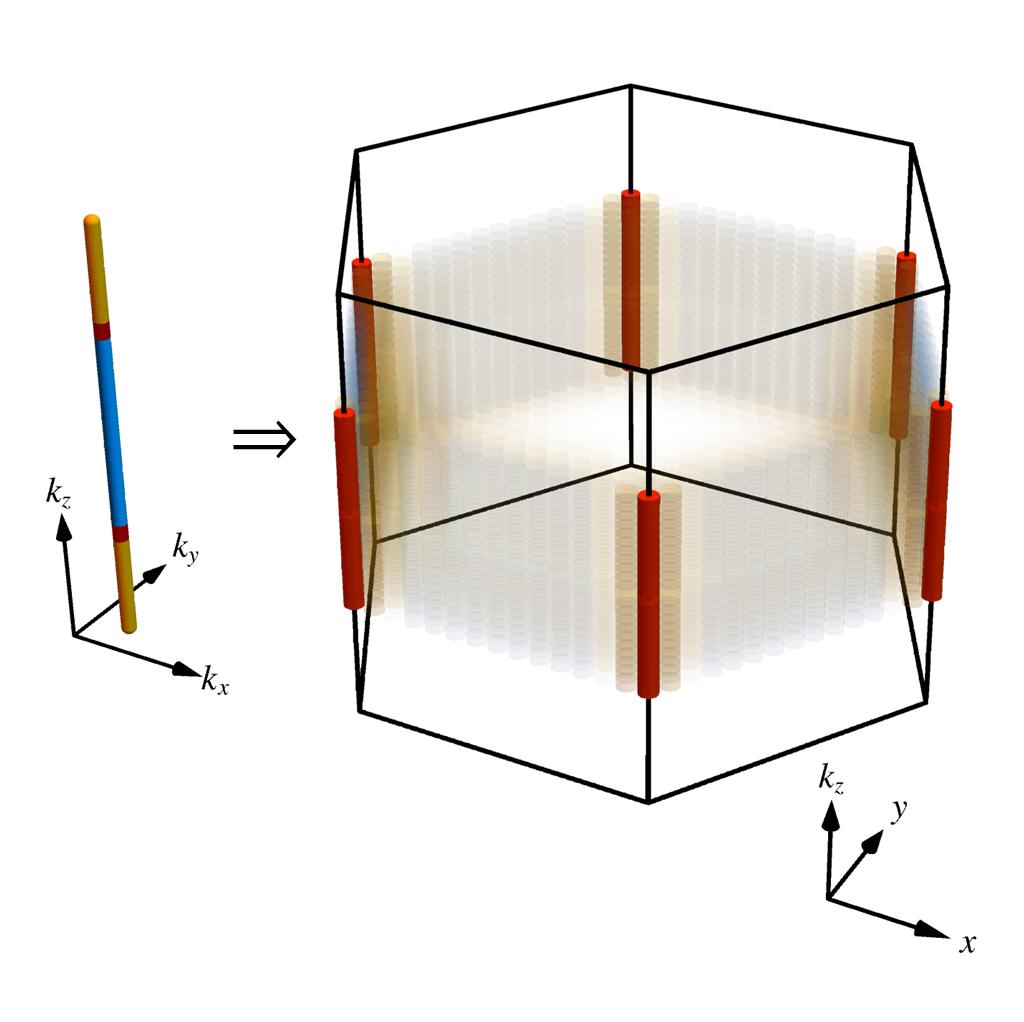
We show that pairs of triple points in systems with negligible spin-orbit coupling (three-fold momentum-space band structure degeneracies along high-symmetry lines) facilitate higher-topology. Our main result is a universal bulk-hinge correspondence of such pairs to fractional quantized jumps of the hinge charge as a function of the hinge-momentum. For the special case of \(\mathcal{P}\mathcal{T}\)-symmetric crystalline solids we further find that triple points are characterized by monople charges. We illustrate the derived phenomena on material examples using first-principles calculations.

Abstract

Triple nodal points are degeneracies of energy bands in momentum space at which three Hamiltonian eigenstates coalesce at a single eigenenergy. For spinless particles, the stability of a triple nodal point requires two ingredients: rotation symmetry of order three, four or six; combined with mirror or space-time-inversion symmetry. However, despite ample studies of their classification, robust boundary signatures of triple nodal points have until now remained elusive. In this work, we first show that pairs of triple nodal points in semimetals and metals can be characterized by Stiefel-Whitney and Euler monopole invariants, of which the first one is known to facilitate higher-order topology. Motivated by this observation, we then combine symmetry indicators for corner charges and for the Stiefel-Whitney invariant in two dimensions with the classification of triple nodal points for spinless systems in three dimensions. The result is a complete higher-order bulk-boundary correspondence, where pairs of triple nodal points are characterized by fractional jumps of the hinge charge. We present minimal models of the various species of triple nodal points carrying higher-order topology, and illustrate the derived correspondence on Sc\(_3\)AlC which becomes a higher-order triple-point metal in applied strain. The generalization to spinful systems, in particular to the WC-type triple-point material class, is briefly outlined.